FXでは破産せずに長く続けることが大切です。
長く続けるための一つの指標、「バルサラの破産確率」の計算式を紹介します。
破産確率とは、オーストラリアのプロトレーダー、ブレント・ペンフォールド氏の著書『システムトレード 基本と原則』で紹介された、「トレードを繰り返した結果、資金が底をつく確率」です。
書にもありますが、もともとは数学者ナウザー・バルサラ氏が考案したもので、「バルサラの破産確率」と呼ばれています。
ただ、「破産の確率」については確率漸化式の1つのパターン問題として高校の数学で習うもので、東京大学の過去問にも取り上げられています。
破産の確率について深く学びたい方は、上記の書籍や「数学 破産の確率」などで検索していくつかのウェブサイトを確認するのもいいと思います。
バルサラの破産確率の導出方法
資金がn円のときの破産確率をQ(n)とします。
勝ったらW円もらえるとし、負けたらL円失うような取引を1回行った後は、
資金は n + W円か、n – L円になっています。
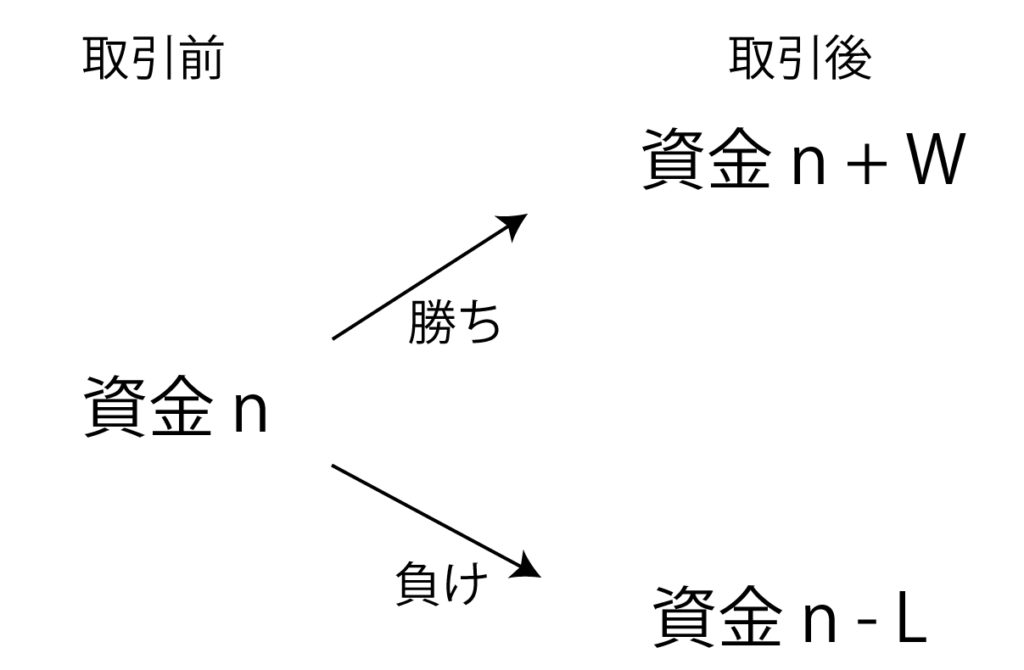
破産する確率を図に表すと、
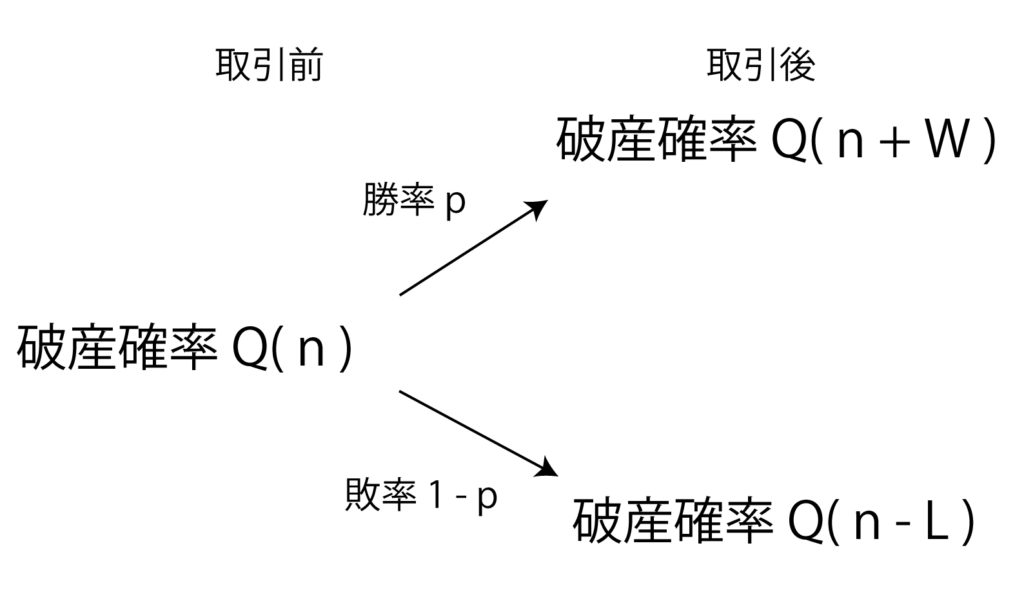
ここで、取引前の破産確率と、取引後の全ての事象の破産確率の和は等しいので、以下の確率変数の式が成立します。
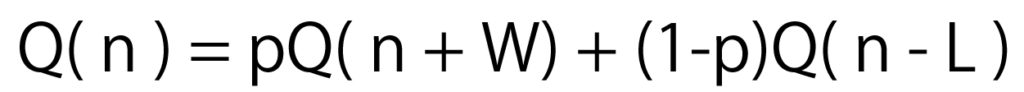
勝ったらWもらえ、負けたらL失うということは、数学的には、
「勝ったらW/Lもらえ、負けたら1失う」ということと等しいので、
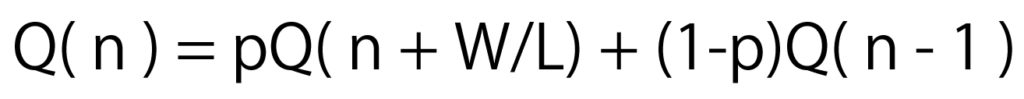
W/Lをkと置き換えると、
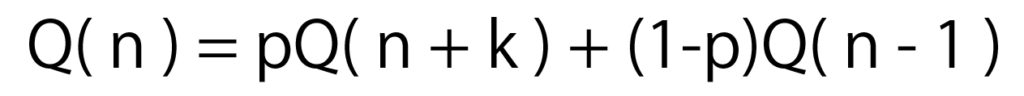
よって、Q(n -1)、Q(n)、Q(n + k)の3つの項からなる漸化式の形に変形できます。
この漸化式の一般項Q(n)を解くには、以下の特性方程式を解きます。
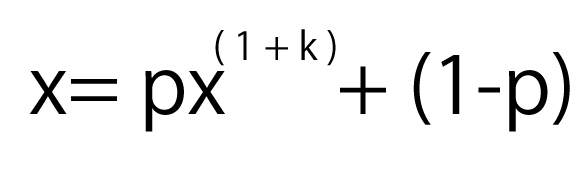
今回はExcel VBAで上記を満たす解xを解きました。
その解をAとおくと、一般項Q(n)(n円のときの破産確率)は、
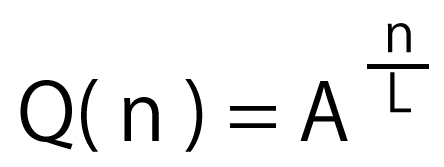
となります。





